For fun, here’s a gallery of graphs derived from master spins.
The approach here is most empirical for the moment.
The idea behind this representation is to exploit the many mathematical tools used in graph theory, and apply them to the measurement of a master spin complexity.
For this, I started converting master spins into directed graphs (the relations between two points are indicated by an arrow).
Each point represents a word (or group of words) and the arrows show the path from one word to another.
To build a text from this representation, we start from the origin and we follow the arrows. If you are faced with several arrows, you chose one, and thereby advance.
NB: this visualization as a graph is not included in the spin synth tool for the moment. It is made from custom algorithms, manual visualizations and use of several tools.
Here are a few representations of similar, quite complex master spins, on two levels:
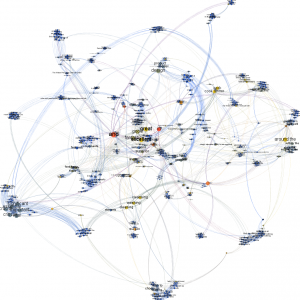
On this graph, we can see by zooming into the use of synonyms: there are linear chains with beams that go from one point to feed 3 or 4, which join to the next, etc… Here, all that is fairly linear has been folded like a ball of wool so that we can have a vision, but the general structure demonstrates the use of synonyms one after the other and not a real complex assembly..

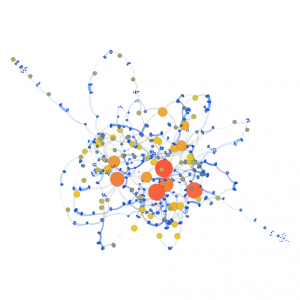
Here is a spin made with spin synth. We recognize the structures of synonyms in chains, which are folded in on themselves; they are spun sentences used as alternatives that make many loops. Towards the center, a large pile of tangled arrows: here was inserted a module that gives a hundred different versions of a text, hence the bushy appearance.
Visually, we clearly discover the imbalance of the text, which includes linear zones and other very dense ones.
We can correct the situation by complicating the portions that require complexity or simplifying the dense ones according to the number of copies needed.
Finally, a big master spin – one we do not often see “in the wild” (also done with spin synth):
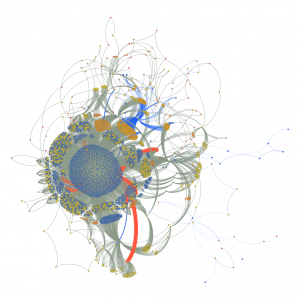
So, what do you think of this representation in the form of a graph? Does it seem useful to you ???
© Spin Synth – forbidden use without authorization.
